| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 안전교육
- 젠센 부등식
- 넘파이
- python#yaml#가상환경#파이썬
- journal club
- numpy
- DCM
- 통계
- 티스토리챌린지
- regret-minimization
- 닫힌 해
- choice model
- 논문 리뷰
- 윤리 및 안전
- Expectation Maximization
- latex#티스토리#tistory#대학원#논문#논문정리
- 대학원
- Closed Form
- 옌센 부등식
- convex
- EM 알고리즘
- 볼록 함수
- em알고리즘#expectation maximization#algorithm
- 나비에 스토크스
- lccm
- 카이스트
- 연구
- jensen's inequality
- discrete choice model
- Python
- Today
- Total
대학원생 리암의 블로그
[논문 리뷰] Random Regret-Based Discrete-Choice Modelling : An Application to Healthcare 본문
[논문 리뷰] Random Regret-Based Discrete-Choice Modelling : An Application to Healthcare
liam0222 2024. 10. 19. 17:33Random Utility Maximization(RUM)은 개인 선택 행동을 모델링하는 기법으로 개인이 가장 높은 utility를 제공하는 alternative를 선택한다는 이론이다. 이 모델의 대안으로 제시되는 것이 Random Regret Minimization (RRM)이며 이는 특정 선택을 했을 때 기회비용(후회)이 가장 적은 alternative를 선택한다는 기법이다. 두 기법을 섞은 방법론이 Hybrid RUM-RRM 모델이며 이는 보상과 후회를 타협하여 고려한다.
기존에는 RUM 방법론이 널리 사용되었으나 해당 논문에서는 최근 교통 경제학에서 사용되는 RRM 접근법을 채용하여 의료정책 분야에 적용해보고자 하였다. 그리고 이를 골다공증 약물 치료와 HPV 백신 데이터를 통하여 성능을 증명하고자 하였다.
Mathematical Formulation
1. RUM (Random Utility Maximization) 모델
RUM 모델에서는 각 대안의 효용 \( U_i \)가 설명 가능한 성분 \( V_i \)와 설명할 수 없는 성분 \( e_i \)로 나뉜다.
\[U_i = V_i + e_i = \sum_{m} \beta_m x_{im} + e_i \tag{1}\]
- \( \beta_m \): 속성 \( x_m \)에 대한 가중치(계수).
- \( x_{im} \): 대안 \( i \)에 대한 속성 \( m \)의 값.
- \( e_i \): 확률적 오차 항으로, i.i.d. Extreme Value Type I 분포를 따른다.
선택 확률 \( P(i) \)는 모든 대안의 효용을 바탕으로 다음과 같은 로짓 함수로 계산된다:
\[P(i) = \frac{\exp(V_i)}{\sum_{j=1}^{J} \exp(V_j)} \tag{2}\]
2. RRM (Random Regret Minimization) 모델
선택된 대안보다 더 나은 대안이 있을 때만 후회가 발생한다. 즉, 선택한 대안이 최선일 때는 후회가 발생하지 않는다.
수식으로는 다음과 같이 표현된다:
\[
R_{i \leftrightarrow j} = \max(0, \beta_m \cdot (x_{jm} - x_{im}))
\]
그런데 해당 방법은 특정 지점 이후로 abrupt하게 그래프가 증가한다. 때문에 logsum 접근법을 사용해서 smoothing을 해준다.
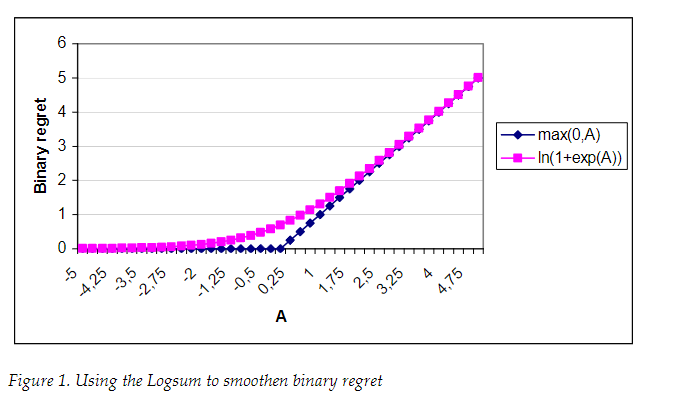
\[\mathbb{E} [R_{i \leftrightarrow j}] = \ln(1 + \exp(\beta_m (x_{jm} - x_{im})))\]
이 공식은 후회를 연속적이고 부드럽게 변화시키며, 음수 후회의 영향은 0에 가깝게 보정해준다. 왜냐하면 exp(-value)는 0에 가깝기 떄문이다.

RRM 모델에서는 IIA assumption이 적용되지 않는다. IIA 가정이란 한 대안을 선택할 확률은 다른 대안들의 속성이나 존재에 영향을 받지 않아야 한다는 원칙이다. 그러나 위 식에서 보이다시피 대안 i와 대안 j 사이의 인기도는 그들 서로 간의 성과뿐만 아니라 대안 k와의 성과에도 의존한다는 것을 볼 수 있다. 또한 비교를 통해 계산이 되기 때문에 no-choice option의 선택했을 때의 해석이 모호하다. 따라서 RRM 모델은 해당 경우 사용하지 않는다.
RRM 모델에서는 대안 간 속성 비교를 통해 발생하는 후회\( RR_i \)가 체계적 성분 \( R_i \)와 무작위 성분 \( e_i \)로 나뉜다.
\[RR_i = R_i + e_i = \sum_{j \neq i} \sum_{m} \ln \left( 1 + \exp \left( \beta_m (x_{jm} - x_{im}) \right) \right) + e_i \tag{3}\]
여기서:
- \( \ln \left( 1 + \exp(\beta_m (x_{jm} - x_{im})) \right) \): 대안 \( i \)와 \( j \) 간 속성 \( m \)에서의 후회 정도.
- \( \beta_m \): 속성 \( x_m \)에 대한 가중치(계수).
- \( e_i \): i.i.d. Extreme Value Type I 분포를 따름.
선택 확률 \( P(i) \)는 각 대안의 후회를 바탕으로 다음과 같은 로짓 함수로 계산된다:
\[P(i) = \frac{\exp(-R_i)}{\sum_{j=1}^{J} \exp(-R_j)} \tag{4}\]
3. Hybrid RUM-RRM 모델
\[ V_i = \sum_{m=1}^{Q} \beta_m x_{im} - \sum_{j \neq i} \sum_{m=Q+1}^{M} \ln \left( 1 + \exp \left( \beta_m (x_{jm} - x_{im}) \right) \right)\]
1번 모델 값 뺴기 2번 모델로 구성되며 probability는 아래와 같이 모델된다.
\[P(i) = \frac{\exp(V_i)}{\sum_{j=1}^{J} \exp(V_j)}\]
RUM과 RRM 모델의 차이
1. 보상 가능성(Semi-compensatory vs. Fully compensatory behavior): RUM 모델은 fully compensatory behavior을 가정한다. 왜냐하면 한 속성에서 성능이 낮아도, 다른 속성에서 뛰어난 성능이 있다면 전체 효용이 클 수 있기 때문이다. 반면에 RRM 모델은 semi-compensatory behavior을 가정한다. RRM은 한 속성에서 매우 낮은 성과를 보이는 경우 큰 후회를 유발하며(마이너스 값), 이는 다른 속성에서 상쇄되지 못 할 수 있다. RUM은 최대값, RRM은 평균값과 유사한 점이 있다고 생각했다. 따라서 RUM 모델에서는 강력한 성과를 보이는 대안이 선호되지만, RRM 모델에서는 성과가 중간인 대안이 더 높은 점유율을 얻게 된다.
2. 계산 복잡성 : RRM은 대안간의 비교로 인해 계산의 복잡성이 높고 추정에 더 많은 시간이 걸린다.
3. 파라미터 해석 :
RRM : 속성 값이 1단위 증가했을 때 대안을 다른 대안과 비교하여 후회가 얼마나 증가하거나 감소하는지를 나타낸다.
RUM : 속성 값이 1단위 증가했을 때 대안의 효용이 얼마나 증가하거나 감소하는지를 나타낸다.
Experiment
모델들을 테스트 하기 위해 두가지 데이터 셋에 실험을 진행했다.
1. 골다공증 예방 약물 치료 데이터
Independent Variables
Attribute 1 - 약물 복용 방법 (Route of drug administration): 월 1회 알약, 주 1회 알약,
Attribute 2 - 주사 주기 : 4개월마다 GP(일반의) 주사, 월 1회 GP 주사
Attribute 3 - 10년간 고관절 골절 위험 감소 (10-year risk reduction of a hip fracture): 5%, 10%, 25%, 50%
Attribute 4 - 부작용 (Nausea) : 없음, 있음
Attribute 5 - 치료 지속 기간 (Total treatment duration): 1년, 2년, 5년, 10년
Attribute 6 - 본인 부담 비용 (Total out-of-pocket costs) : €0, €120, €240, €720
Dependent Variables
종속 변수는 각 대안 중 참가자가 실제로 선택한 항목이다.
골다공증 예방 약물 치료 DCE에서는 참가자들이 3가지 대안 중 하나를 선택한다 : 약물 치료 대안 1, 약물 치료 대안 2, 약물 치료를 하지 않는 대안 (opt-out)
2. HPV 백신 데이터
Independent Variables
Attribute 1 - 자궁경부암 예방 효과 (Protection against cervical cancer): 50%, 70%, 90%
Attribute 2 - 효과 지속 기간 (Protection duration): 6년, 25년, 평생
Attribute 3 - 심각한 부작용 확률 (Serious side effects): 1:750,000, 1:150,000, 1:30,000
Attribute 4 - 경미한 부작용 확률 (Mild side effects): 1:50, 1:30, 1:10
Dependent Variables
백신 접종 대안 1, 백신 접종 대안 2, 백신 접종을 하지 않는 대안 (opt-out)
Result
Table 1. Osteoporosis drug treament coefficient

Table 2. HPV coefficient

Monte Carlo Simulation을 1000번 동안 반복해서 panel logit model의 coefficient를 유추했다.
골다공증 데이터셋 결과 해석:
- 속성 변화 영향:
- 메스꺼움(nausea)이 '없음'에서 '있음'으로 변화할 때:
- RUM 모델: 33.9%의 추가적인 10년 hip 골절 위험 감소 또는 €655의 추가 비용 감소가 필요
- RRM 모델: 28.4%의 추가 위험 감소 또는 €662의 추가 비용 감소가 필요
- 모델 적합도:
- RRM 모델이 데이터에 더 나은 적합도를 제공하며, Hybrid RUM-RRM 모델보다 (p < 0.02) 유의미한 차이가 있었으나 RUM 모델과의 차이는 유의하지 않았다 (p < 0.21).
- 모든 속성이 예방적 치료에 대한 환자 결정에 유의미한 영향을 미쳤다 (p < 0.05).
- 교환 비율 및 보상:대안을 비교할 때 교환 비율을 분석한 결과 보상을 평준화하는 데 필요한 비용 감소가 다르게 나타났다 :
- Treatment A의 메스꺼움이 '0'에서 '1'로 증가했을 때 €668의 비용 감소가 필요했다.
- Treatment A는 메스꺼움이 없고 Treatment B와 C는 메스꺼움이 있을 경우, €550의 더 적은 감소가 필요했다.
- 매개변수 비율:
- 메스꺼움과 다른 속성 간의 매개변수 비율 차이는 작았으며(±€7) 통계적으로 유의미하지 않았다.
HPV 예방접종 결과 해석:
- 속성 변화 영향:예방접종 연령이 '14세'에서 '9세'로 변경될 경우:
- RUM 모델: 4.2%의 추가 자궁경부암 예방 효과 또는 7.9년의 추가 보호 기간이 필요하다.
- Hybrid RUM-RRM 모델: 5.6%의 추가 예방 효과 또는 6.9년의 추가 보호 기간이 필요하다.
- 모델 적합도:
- Hybrid RUM-RRM 모델이 RUM 모델 (p < 0.05)과 RRM 모델 (p < 0.01)보다 약간 더 나은 적합도를 나타냈다.
- 통계 분석:
- 추가 분석 결과, 모델 간의 비율에 유의미한 차이는 없었으며, 예측 결과에서 차이가 나타났다.
Conclusion
RRM 모델은 성능이 다른 대안들에 비해 중간 정도에 해당하는 타협 대안에 대해 더 높은 선택 확률을 보였다. 이는 소비자 심리학 연구에서 관찰된 결과와 일치하며, RRM 모델의 반보상적 성격(semi-compensatory nature) 때문에 발생한다.
따라서 행동 예측이 정책 목표라면, 데이터 적합도가 더 좋은 경우 RRM 모델이 더 나은 정책 평가 도구가 될 수 있다. 하지만, 사회적 복지 극대화가 목표라면 RUM 모델이 더 적합할 수 있다.




