[논문 리뷰] Smooth Multi-Period Forecasting With Application to Prediction of COVID-19 Cases

---

---

Intro

 

본 논문은 2024년 1월에 Journal of Computational and Graphical Statistics에 실린 논문이다. 논문의 저자들은 카네기 멜론 Delphi Group 소속이며 전염병 관련 forecasting 및 analytics 관련 연구를 활발히 하고 있다. 

 

 Tuzhilina, E., Hastie, T. J., McDonald, D. J., Tay, J. K., & Tibshirani, R. (2024). Smooth multi-period forecasting with application to prediction of COVID-19 cases. Journal of Computational and Graphical Statistics, 33(3), 955-967.

---

Aim

 

저자들은 자신들이 개발한 과거 데이터 기반 다중 기간 예측(Multi-Period Forecasting, MPF) 방법론을 소개한다. 본 모델을 통해 더욱 정밀한 코로나 감염자 수를 예측하는 것을 목적으로 한다.

---

Literature Review

 

시계열 예측에 사용되는 대표적 모델들을 나열하며 해당 모델이 가지는 차별점을 설명한다. 아래가 사용되고 있는 대표적인 모델들이다. 

1) Box-Jenkins 모델 (Box & Jenkins, 1976)

– 자기회귀(AutoRegressive, AR), 이동평균(Moving Average, MA), ARMA, ARIMA 등의 회귀 기반 방법.

– 과거 값들의 선형 결합으로 표현되는 모델

– 비선형적인 경우 예측력이 떨어짐

2) 딥러닝 및 기계학습 접근법

– ANN & LSTM 등의 모델들은 비선형 데이터에 유용하지만 해석성이 떨어짐 (Siami-Namini et al., 2018).

 

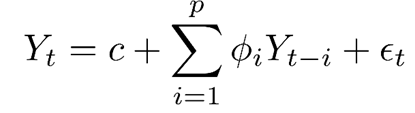
이러한 모델들은 보통 single forecast horizon 예측에 사용되는 경우가 많으나 코로나 관련 연구처럼 future trend 역시 중요한 epidemology domain에서는 multi-period forecasting 역시 필요해졌다. 

---

다중 기간 예측(Multi-Period Forecasting) 접근법에는 두가지 방식이 있을 수 있다.

 

i) 첫번째는 단일 출력 예측(Single Output Model) 방식이다.

한 단계씩 순차적으로 다음 period의 값을 예측하는 방식이다. 예측값을 다시 입력 변수로 사용하여 다음 값을 예측하는 방식이기에 기존의 single forecast horizon 방법론을 그대로 가져다가 사용할 수 있다는 점에서 용이하나 error propagation 문제에 prune하다.

 

ii) 두번째 방법은 다중 입력 다중 출력(MIMO, Multiple-Input Multiple-Output)이다.

이는 여러 개의 미래 값을 한꺼번에 예측하는 방법이다 (Bontempi, 2008). 그러나 기존의 연구들은 미래 값들을 서로 독립적으로 예측하여 예측값들 사이의 트렌드를 포착하는데는 적합하지 않았다. 이러한 문제점에서 착안해서 본 논문은 개별 시점 예측을 따로 하는 것이 아니라 연속적인 여러 미래 시점을 동시에 예측하는 방법론을 제안한다. 구체적으로 모든 예측값들이 하나의 공통된 basis function으로부터 나온다고 설정하고 fitting을 한다. 그리고 그 하나의 smooth function으로부터 모든 예측 값들을 추정한다. 

---

Baseline Model

 

우선 기준이 되는 baseline model을 설정한다. 

 

Dependent variable(Y)은 발생하는 코로나 환자수이고 independent variable은 p개의 covariate으로 이루어진 vector이다. 그런데 시계열 분석의 특성상 과거 정보를 활용하기에 얼마나 과거의 정보를 사용할 것인지를 time lag L로 표현한다. 예를 들어 7일전과 14일전 데이터를 사용한다면 L의 집합은 {7, 14}가 되는 것이다. 또한 어떤 미래의 horizon을 예측할 것인지를 horizon 집합 A로 나타낸다. 예를 들어 10일과 14일 뒤의 Y값을 예측하고자 하면 horizon 집합 A는 {10, 14}가 될 것이다.

---

위 notation을 활용해서 baseline model을 아래와 같이 formulate 할 수 있다.

 

t라는 시점에서 a라는 horizon 뒤의 i지역의 코로나 발생자 숫자를 예측하는 것은 coefficient b(a)와 x의 선형결합으로 표현할 수 있다. 이때 feature X는 p개의 covariate으로 이루어져 있으며 time lag 집합에 있는 모든 시점의 값을 다 사용한다.

---

그리고 coefficient는 Ordinary Least Squares Regression을 푸는 것으로 찾아낼 수 있다. 모든 coefficient b(a)를 각각 탐색하게 된다. 

---

Smooth Multi-Period Forecasting (SMPF) Model

 

위 baseline 모델은 예측 대상이 되는 여러 시점(horizons)별로 coefficient를 독립적으로 계산함. 그러나 같은 정보(signal)를 통해 서로 다른 미래 시점(t+a)에 대해 예측이 진행되는 것이므로 예측값들을 부드럽게 연결시키면 trend 정보를 활용할 수 있을 것이다. 따라서 SMPF는 계수 b(a)가 a에 dependent한 smooth 함수로 표현되게 강제한다. Smooth 함수로는 spline 또는 polynomial 등으로 사용한다. 

 

위에서 보여지는 것처럼 동일한 covariate k에 대해서는 h(a)라는 공통된 basis smooth function을 사용하고 theta만 따로 fitting하는 방식을 채택한다. 기존의 방식인 동일한 covariate k에 대해서도 different time horizon 마다 개별적으로 fitting한 것과 다른 방식이다. 

---

그래서 optimization 식을 한눈에 비교하면 아래와 같다. 

---

Extension to Quantile Estimation

 

여기서 한 단계 더 나아간 refinement를 적용하게 된다. Baseline MPF 모델은 평균 값을 예측하는 데 초점을 맞추고 있다. 그러나 epidemic prediction은 실제 데이터에서 오차가 클 수가 있기에 상한과 하한을 제공하는 방식으로 확장시키면 더 다양한 시나리오에 대비할 수 있다. 또한 부가적인 장점으로는 outlier에 robust하다는 것과 오차가 정규분포를 따르지 않아도 된다는 것이다. 

 

Quantile을 추정하기 위해 pinball loss function을 적용한다. 

---

쉽게 설명해서 예측값이 실제보다 작으면 tao만큼의 penalty를 주고 더 크면 1-tao만큼의 penalty를 준다. 이렇게 되면 tao가 0부터 1사이의 값일 때 tao의 quantity에 해당하는 quantile의 값을 예측하게 된다. 그 증명을 아래와 같고 궁금하면 참고하면 좋을 것 같다. 증명은 특정 tao가 주어졌을 때 어떤 y hat을 estimate해야 실제 값 y에 대한 pinball loss의 expectation이 최소화 되는지를 통해 이루어진다.

 

---

 

Conformal Calibration

Quantile estimation은 sampling을 통해서 이루어지기 때문에 estimated 값이 실제 신뢰 구간과 일치하는지 비교하고 오차를 일부 보정해줄 수 있다. 예를 들어, 구간을 τ=0.2~0.8로 적용했음에도 불구하고 실제 데이터를 포함하는 비율이 60%보다 작거나 크다면 calibration을 통해 신뢰구간을 60%에 가깝게 조정할 수 있다.

구체적인 절차는 다음과 같다. 우선 아래의 pinball optimization 식을 통해 y hat을 추정한다.  

 

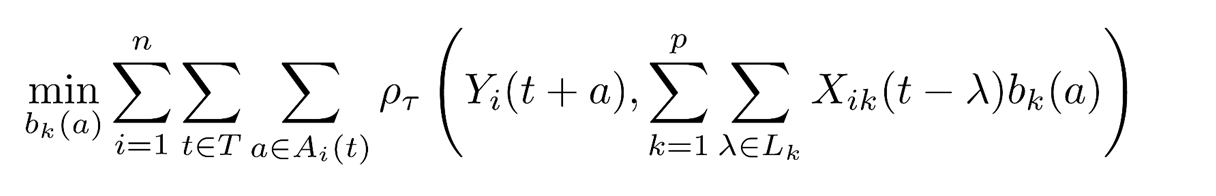
추정된 beta coefficient를 활용해서 E로 표현되는 error들을 구할 수 있다. 

 

---

그렇게 되면 지역 i의 모든 horizon에해 해당하는 Error set을 구할 수 있다. 

---

그 이후 Q라는 보정 상수를 구하게 된다. 식은 아래와 같다. 

---

 

하한선은 보정상수를 더해주고, 상한선에서는 보정상수를 빼줌으로써 quantile의 coverage가 더 정밀하게 보정해줄 수 있다.  내가 헷갈렸던 건 하한선 Y tao를 구할 때 왜 1-tao구간의 error를 더해주는 것이냐는 거였는데 예시로 생각하니 편해졌다. Error가 predicted y - actual y로 계산되기 때문에 하한 20%를 기준으로 예측한 predicted y는 대부분 음수인 error set을 줄 것이다. 예를 들면 이런식일것이다. 

 

{-7, -6, -5, -4, -3, -2, -1, 0, 1, 2}.

 

이처럼 물론 값은 오른쪽으로 갈수록 증가하지만 error의 magnitude자체는 오른쪽으로 갈수록 작아진다. 따라서 subtle한 보정을 위해서는 error중에 80% 구간인 '0'을 더해주는 것이 합리적일 것이다. 이는 상한선에도 동일하게 정의된다. 

---

Simulation Experiment

 

해당 모델의 성능을 확인하기 위해 synthetic data를 만들고 테스트한다. 조건은 다음과 같다.

---

이 과정을 graphical하게 살펴보면 다음과 같다.

우선 3개의 전 시점을 기준으로 각각의 covariate이 autoregressive하게 영향을 받으며 존재한다. 5개의 선은 각각 하나의 covariate을 뜻한다. 50 time stamp를 train, 그 뒤의 50개의 time stamp를 test로 사용한다. 

---

 또한 coefficient(b)는 3차식을 기준으로 설정이 되었다. 그리고 맨 아래 사진에서 보이듯이 위 x와 b를 곱해서 y를 예측하게 된다. 

---

 

이렇게 생성한 데이터를 바탕으로 baseline mpf와 smpf를 비교한다. 그런데  이미 Y를 generate 하기 위해서 사용된 식에서 볼 수 있듯이 H matrix가 스무딩 형식을 띄고 있음. 그래서 결과 자체가 SMPF가 더 좋게 나오긴 하는데 개인적으로는 단순히 데이터 생성 방식과 모델의 특성이 잘 맞았기 때문일 가능성이 크다고 생각하여 의미가 없다고 생각한다. 그래도 논문에서는 실제 데이터로 테스트한 실험을 추가하여 신빙성을 더하고 있다.

---

Real Data Experiment

 

COVIDcast API에서 데이터를 가져왔으며 독립변수는 다음과 같다 :

 

1. confirmed_7dav_incidence_prop (Lagged)

- 일일 신규 확진자 수 (100,000명당 발생률 기준)

- 예측하고자 하는 반응 변수(Response Variable)

 

2. smoothed_cli

- COVID-like illness (코로나 유사 질환) 비율

- Facebook과 Carnegie Mellon University가 수행한 조사 데이터

 

3. smoothed_hh_cmnty_cli

- 지역사회 내 질병 발생 비율

- 동일한 조사에서 측정된 데이터

 

 종속 변수는 다음과 같다 : 

 

1. confirmed_7dav_incidence_prop

- 일일 신규 확진자 수 (100,000명당 발생률)

---

데이터 개요

 

• 훈련 데이터 : 2021년 7월 10일 ~ 10월 1일 (총 12주)

• 테스트 데이터: 2021년 10월 2일 ~ 10월 29일 (4주간 예측 평가)

• 모든 지표는 7일 이동 평균(smoothing) 처리하여 주별 변동성을 제거 => 기준 일 전 3일과 기준일 뒤 3일의 평균을 사용

• Time Lag : \( L = \{1,2,3,\dots,28\} \)

• Time Horizon : \( A = \{0,1,\dots,27\} \)

 

---

이를 시각적으로 보면 아래와 같다 :

• 파란색 (observed train)
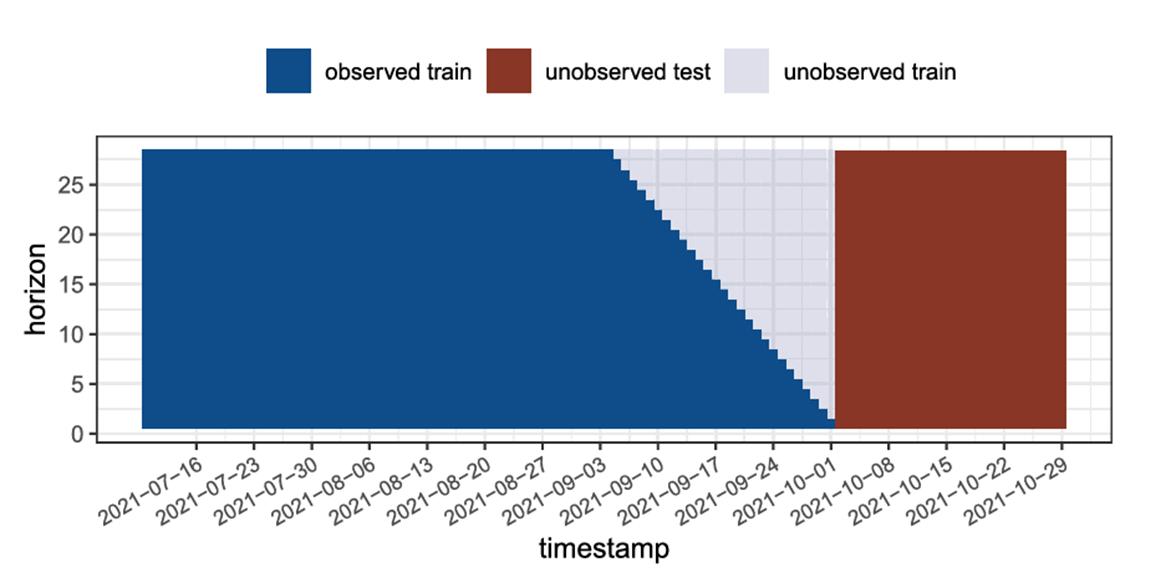
→ 2021년 7월 16일~10월 1일까지의 완전한 훈련 데이터

• 갈색 (unobserved test)
→ 2021년 10월 2일 이후 미래 데이터 (테스트 세트)
→ 이 데이터는 훈련 과정에서는 사용할 수 없으며, 오직 모델 성능 평가를 위해 사용됨.

• 회색 (unobserved train)
→ 미래의 horizon 값들이 포함되면서 생긴 결측 데이터

---

Real Data Result

결측치가 있어도 imputation을 0으로 넣고 사용한 것이 아예 결측치 데이터를 빼버리는 것보다 나은 성능을 보였으며 degree가 2 이상일 때부터는 SMPF이 MPF 보다 더 좋은 성능을 보인다. 그 이유는 degree가 1일 때 Baseline MPF 모델은 개별 horizon을 독립적으로 예측하므로 선형 제약이 없는 반면 Smooth MPF 모델은 모든 horizon을 하나의 선형 함수로 표현하려고 하여 너무 단순화 된 예측으로 이어지기 때문이다. 또한 degree가 3이상부터는 되려 test mae가 올라가는데 이는 over-fitting의 영향이라고 말하고 있다. 

---

 

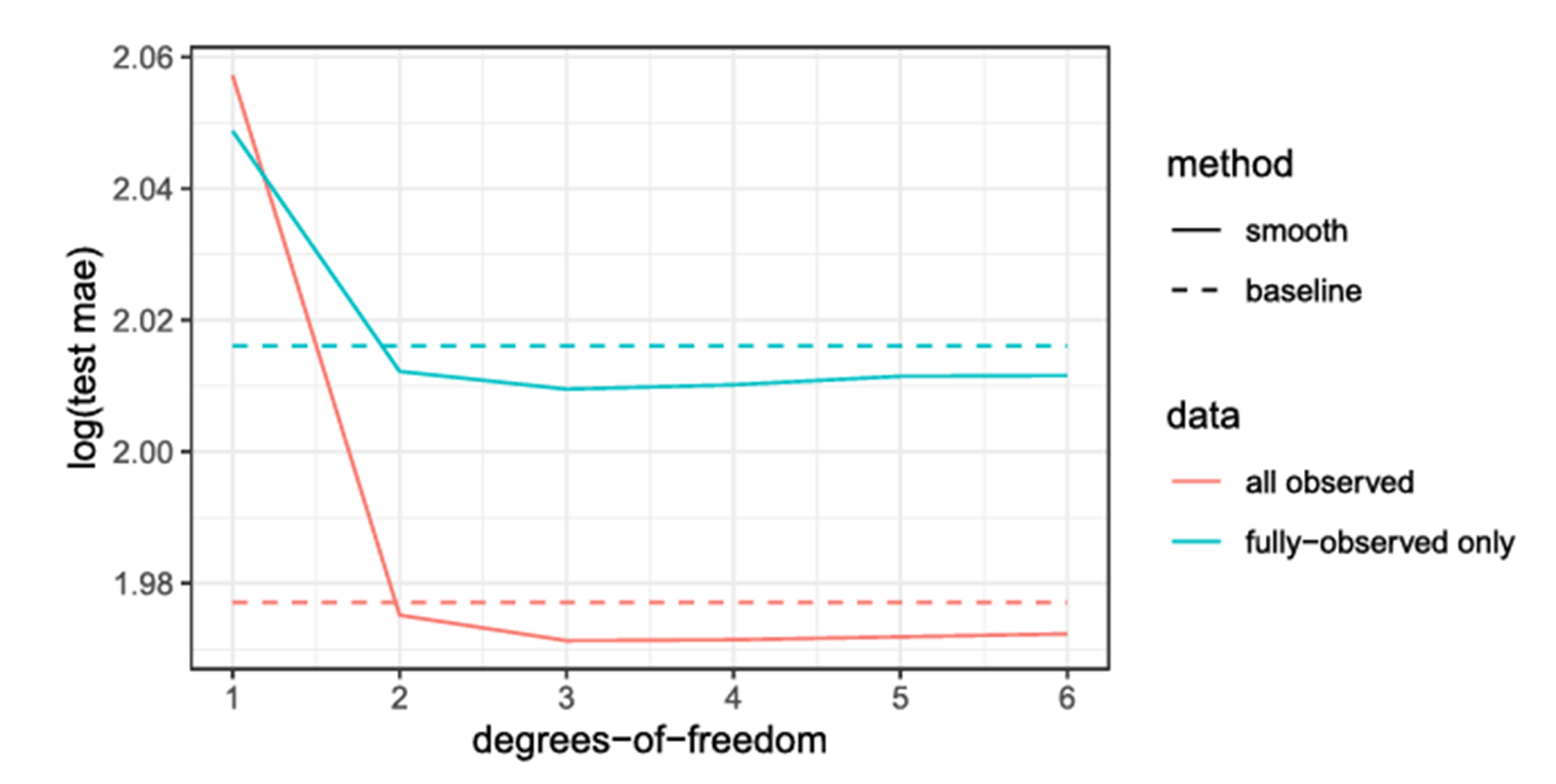
또한 결과를 horizon 값이 바뀜에 따라 어떻게 MAE가 변화하는지를 중심으로도 살펴볼 수 있다. 몇가지 결과를 살펴볼 수 있는데 첫번째로는 Horizon이 커질수록 Test MAE 증가한다는 것이다. 이는 미래로 갈수록 예측이 어려워지고, MAE(오차)가 증가한다는 것이다. 특히, Baseline 모델(주황색)은 다른 모델들보다 비교적 일정한 증가율을 보임. 또한 노란색 선(Smooth 1)은 다른 모델들보다 전반적으로 높은 MAE를 보이는데 이는 앞서 언급한 바와 같이 너무 단순한 모형이라 예측 성능이 좋지 않기 때문이다. 15일 이후에는 SPMF 모델이 baseline과 유사한 오차를 보이지만, 그래도 baseline보다는 더 낮은 에러율을 보인다. 

---

Result shown in panel form

또한 예측 결과를 county 별 panel graph로도 그려볼 수 있다. 위 그래프는 가장 많은 평균 사례 수를 기록한 20개 카운티(county)에 대한 Baseline 모델과 d=3을 사용한 최적의 Smooth 모델의 예측 결과를 비교한다. 예측은 2021년 10월 2일 데이터를 기준으로 수행되며 각각이 뜻하는 바는 아래와 같다 :

• 굵은 검은 선(Bold Line): 실제 관측된 신규 보고 감염 사례.

• 가느다란 선(Thin Lines): 모델이 예측한 값. (초록이 SMPF, 보라가 PMF)

• 음영 영역(Shaded Region): 0.2와 0.8 분위수(Quantiles)를 사용하여 생성된 예측 구간 (초록이 SMPF, 보라가 PMF).

그리고 위 그래프를 통해 몇가지 관측 결과를 도출할 수 있었다. 

1️⃣ Smooth 모델이 baseline QMPF보다 더 부드러운 예측을 제공하며 모델이 데이터 패턴을 더 잘 학습하고 있음을 시사한다. (그런데 당연한 거 아닌가라고 생각했다. smoothing function을 강제하기 때문에..)

2️⃣ 일부 카운티에서 Baseline이 과적합(Overfitting)하는 경향이 있었다. 일부 패널(예: 01097, 12083, 45035)에서 보라색 선이 실제 값(검은색 선)을 지나치게 따르려는 과적합의 모습을 보여줌의 반면 Smooth QMPF는 전체적인 패턴을 따르는 더 일반화된 예측을 보였다. 

 

3️⃣ Smooth QMPF의 신뢰 구간(녹색 음영)이 Baseline보다 일관됨을 확인할 수 있었다. Baseline QMPF의 신뢰 구간(보라색 음영)은 일부 카운티에서 매우 넓어지거나 불안정한 형태(fluctuations)를 가짐. 반면, Smooth QMPF의 신뢰 구간(녹색 음영)은 좀 더 일관된 폭을 유지하며, 안정적인 예측을 제공하고 있다. 또한 전반적으로 Smooth 모델이 예측 성능을 향상시켰다(85%).

---

Comparison to other models

 

마지막으로 저자들은 해당 모델을 다른 모델의 performance와 비교를 하는데 SQMPF가 성능면에서 가장 우월하지는 않지만 그래도 comparable하며 설명가능하다는 점을 강조하고 있다. 사용된 지표는 WIS로 이는 예측값뿐만 아니라, 예측의 신뢰구간(uncertainty)까지 고려하는 평가 방식이다. 비교 모델들은 다음과 같다 :

 

CDC Ensemble : 다양한 개별 모델(통계 모델 + 머신러닝 + 일부 딥러닝) 조합

CMU-TimeSeries : 완전히 설명 가능한 전통적인 시계열 모델 기반

Deep Learners : LSTM, GRU, Transformer 등 딥러닝 모델 활용